Back to TILs

C++ Complex Number — 01

Date: 2023-03-10Last modified: 2024-11-02

C++complex norm abs imag real

CC-BY-SA-3.0 diagram by Daniele Pugliesi on Wikimedia

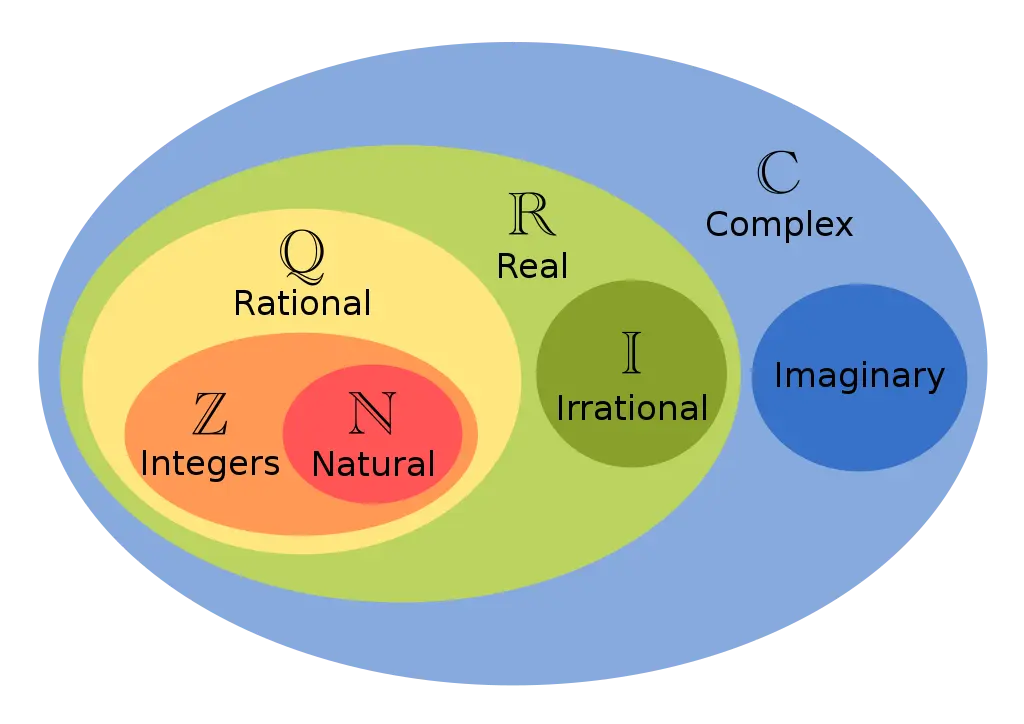
Table of contents

Complex Number
Functions
Norm vs Abs
Possible output
References

Complex Number

Functions

real: Real part of complex
imag: Imaginary part of complex
abs: Absolute value of complex
arg: Phase angle of complex
norm: Norm of complex
conj: Complex conjugate
polar: Complex from polar components
proj: Complex projection.

Norm vs Abs

In essence, the absolute value of a real number captures the idea of its magnitude, i.e., its distance to the origin $0$ on the real number line, ignoring its algebraic sign (positive or negative).

When you try to generalise this to multi-dimensional vectors, the most natural extension that captures the idea of distance to the origin is the Euclidian norm, also known as the $L^{2} - n o r m$ . It consists of the square root of the sum of squares of the coordinates of the vector, as that also measures its magnitude, or the distance between the tip of that vector and its base if that base is made to be the origin.

x = (x_{1}, x_{2}, \dots, x_{n})

L^{2} - n o r m = | x | = \sqrt{\sum_{k = 1}^{n} | x_{k} |^{2}}

Just like the absolute value chooses to ignore the algebraic sign of a real number in order to capture its magnitude, the Euclidian norm chooses to ignore the direction of the vector and captures its magnitude.

However, one can choose other norms in multi-dimensional space, as long as some rules are satisfied (these are spelled out on the Wolfram page above). Two notable ones are the $L^{1} - n o r m$ which is the sum of the absolute values of the coordinates of the vector, and the $L^{\infty} - n o r m$ which captures the magnitude of the largest of the coordinates of the vector.

The $L^{2} - n o r m$ has been preferred for many computational and optimisation purposes, due to its nice analytical properties, i.e., it has nice closed forms for its gradient when trying to minimise or maximise it. This is the reason the $L^{1} - n o r m$ has been spurned for a long time, due to its “less nice” mathematical properties.

This is now changing thanks to the available computational capabilities, which let us find minima and maxima of objective functions through searches within the desired space, even when there is no nice closed form solution or quite as nice analytical properties to the norm, when compared to the Euclidian norm.

  auto printZ = [](const auto& label, const auto& Z) {
    fmt::print("{:30}=> {}{:+}i\n", label, Z.real(), Z.imag());
  };
  auto printR = [](const auto& label, auto R) {
    fmt::print("{:30}=> {}\n", label, R);
  };

  std::complex<double> z3_4(3.0, 4.0);  // 3 + 4i
  std::complex<double> z1_2{1.0, 2.0};  // 1 + 2i
  std::complex<double> z4_3{4.0, 3.0};  // 4 + 3i
  printZ("z3_4", z3_4);
  printZ("z1_2", z1_2);

  // Addition
  auto sum = z3_4 + z1_2;  // 4 + 6i
  printZ("z3_4 + z1_2, sum", sum);

  // Subtraction
  auto diff = z3_4 - z1_2;  // 2 + 2i
  printZ("z3_4 - z1_2, difference", diff);

  // Multiplication
  auto prod = z3_4 * z1_2;  // -5 + 10i
  printZ("z3_4 * z1_2, product", prod);

  // Division
  auto quot = z3_4 / z1_2;  // 2.2 - 0.4i
  printZ("z3_4 / z1_2, quotient", quot);

  // Conjugate
  auto conj = std::conj(z3_4);  // 3 - 4i
  printZ("conj(z3_4), conjugate", conj);

  // Absolute value (modulus)
  double abs_z3_4 = std::abs(z3_4);  // 5
  printR("abs(z3_4), modulus", abs_z3_4);

  // The norm value of a complex number is its squared magnitude, defined as
  // the addition of the square of both its real and its imaginary part
  // (without the imaginary unit). This is the square of abs(x).
  double norm_z3_4 = std::norm(z3_4);  // 25
  printR("norm(z3_4), norm", norm_z3_4);

  // The phase angle of a complex number is the angle the theoretical vector to
  // (real,imag) forms with the real axis (i.e., its arc tangent). It returns
  // the same as: atan2(x.imag(),x.real());
  double arg_z4_3 = std::arg(z4_3);
  printR("arg(z4_3), phase angle in rad", arg_z4_3);

  // The projection of z onto the Riemann sphere.
  printZ("proj(z1_2)", std::proj(z1_2));
  printZ("proj(z3_4)", std::proj(z3_4));
  std::complex<double> inf1{INFINITY, 50};
  std::complex<double> inf2{-INFINITY, 50};
  std::complex<double> inf3{0, -INFINITY};
  printZ("proj(inf1)", std::proj(inf1));
  printZ("proj(inf2)", std::proj(inf2));
  printZ("proj(inf3)", std::proj(inf3));

Possible output

z3_4                          => 3+4i
z1_2                          => 1+2i
z3_4 + z1_2, sum              => 4+6i
z3_4 - z1_2, difference       => 2+2i
z3_4 * z1_2, product          => -5+10i
z3_4 / z1_2, quotient         => 2.2-0.4i
conj(z3_4), conjugate         => 3-4i
abs(z3_4), modulus            => 5
norm(z3_4), norm              => 25
arg(z4_3), phase angle in rad => 0.6435011087932844
proj(z1_2)                    => 1+2i
proj(z3_4)                    => 3+4i
proj(inf1)                    => inf+0i
proj(inf2)                    => inf+0i
proj(inf3)                    => inf-0i

C++ Complex Number — 01

Complex Number

Functions

Norm vs Abs

Possible output

References