Back to TILs

Otimização numérica em C++

Date: 2020-06-15Last modified: 2023-02-17
C++otimizaçãooptimlibdifferential evolution

A OptimLib é uma biblioteca C++ lightweight para otimização numérica de funções não lineares.

Table of contents

Instalação da optimlib

git clone https://github.com/kthohr/optim.git
cd optim
./configure --header-only-version

Após os comandos acima é criado um diretório chamado header_only_version. A partir daí é só incluir este diretório nos flags de compilação: -Ialgum-lugar/header_only_version

Exemplo 1

Neste exemplo usaremos o método Differential Evolution (DE) que é uma busca genética estocástica para otimização global.

Localizar o mínimo da função f(x)=x2−5x+6.

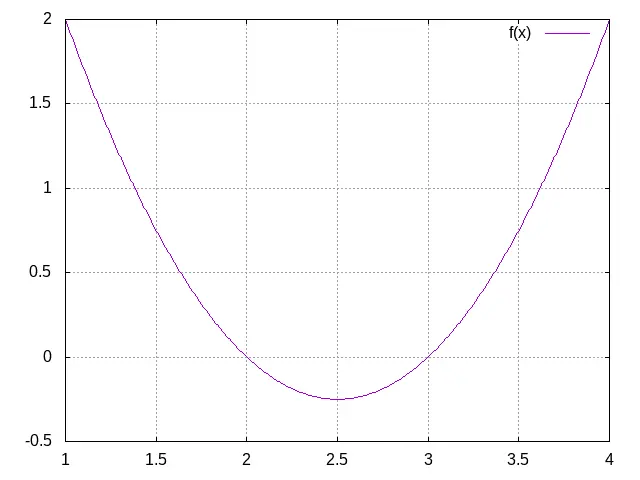
Função exemplo para busca do mínimo.
Fig. 1 - Função exemplo para busca do mínimo.

A função a ser otimizada precisa ter o seguinte formato:

double f( vetor_de_entrada,
          vetor_de_gradiente,
          parametros_adicionais )

Definindo nosso f(x) usando o formato acima:

double f( const arma::vec &vals_inp,
          arma::vec *grad_out,
          void *opt_data )
{
  // Nosssa função é muito simples e só utiliza uma entrada
  const double x = vals_inp( 0 );
  return x * x - 5 * x + 6;
}

Realizando a otimização:

arma::vec x = arma::ones( 1, 1 ) + 0.5; // Valor inicial 1.5
if( optim::de( x, f, nullptr ) ) {
  cout << "Mínimo para f(x): "
       << "x² - 5x + 6 => " << x << endl;
  // Mínimo para f(x) = x² - 5x + 6 => 2.5000
}

Exemplo 2

A função anterior é muito bem comportada e sem mínimos locais. Vamos complicar um pouco.

Localizar o mínimo da função h(x)=x2−5x+6+0.2sin⁡(10x).

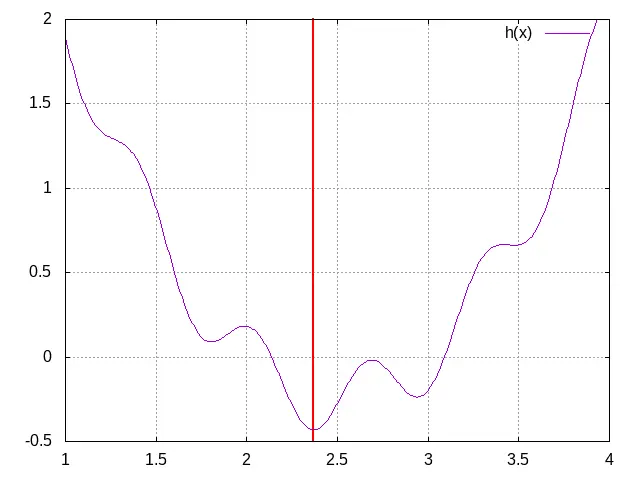
Cálculo do valor mínimo.
Fig. 2 - Cálculo do valor mínimo.

Definindo a nova função:

double h( const arma::vec &vals_inp,
          arma::vec *grad_out,
          void *opt_data )
{
  const double x  = vals_inp( 0 );
  return x * x - 5 * x + 6 + 0.2 * sin( 10 * x );
}

Realizando a otimização:

arma::vec x = arma::ones( 1, 1 ) + 0.5; // Valor inicial 1.5
if( optim::de( x, h, nullptr ) ) {
  cout << "Mínimo para h(x): "
       << "x² - 5x + 6 + 0.2 sin( 10x ) => "
       << x << endl;
  // Mínimo para h(x): x² - 5x + 6 + 0.2 sin( 10x ) => 2.3693
}

Referências