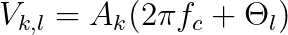QAM (Quadrature Amplitude Modulation)
-
Digital Modulation Techniques Using MATLAB Script file and Graphical Approach
-
has been widely adopted because of its large bandwidth and power efficiency
-
[[4-QAM]] / QAM4
-
[[16-QAM]] / QAM16
-
[[64-QAM]] / QAM64

Quadrature Amplitude Modulation or QAM is a digital modulation scheme where data is transmitted over the channel by varying both the amplitude and phase of the high-frequency carrier signal. The transmitted signal is represented in a constellation plot that contains two axes namely the in-phase and Quadrature. The in-phase and Quadrature axis are separated from each other by a phase of 90˚. Therefore, these two axes are orthogonal to each other.
In the QAM scheme, two or more bits are grouped together to form a symbol that lies in the constellation plot. Each symbol, also called state, has a unique amplitude and phase level that provides distinction across different points in the constellation. Since, the modulation scheme uses binary data, the number of possible bits that can be transmitted can be given by the following equation:
M = 2^N
where N represents the number of bits and M is the number of possible combinations corresponding to any given number of N bits i.e the number of constellation points. Since the value of 2N is also an integer, the total number of bits that can be transmitted is given by,
N = log2 M
QAM Modulation is also known as M-ary QAM where M can be the number of bits represented in the constellation diagram. Some examples include 16-QAM, 32-QAM, 64-QAM, 256-QAM, 1024-QAM, and 4096-QAM.
| Modulation Scheme | Bits/Symbol | Incremental Capacity Gain |
|---|---|---|
| BPSK | 1 | |
| QPSK / 4-QAM | 2 | |
| 8-QAM | 3 | 50% |
| 16-QAM | 4 | 33% |
| 32-QAM | 5 | 25% |
| 64-QAM | 6 | 20% |
| 128-QAM | 7 | 17% |
| 256-QAM | 8 | 14% |
| 512-QAM | 9 | 13% |
| 1024-QAM | 10 | 11% |
| 2048-QAM | 11 | 10% |
| 4096-QAM | 12 | 9.77% |